原创 | 今年冬天,中国严阵以待......
- 国际
- 14小时前
- 1048
4676字7图,阅读大约需要10分钟。
欢迎朋友圈与微信群转发,平台转载请查看主页“联系我们”。
最近商务部发布通知,鼓励家庭储备必要生活物资,这个通知成为最火热的新闻,很多读者留言问我的看法,这里就这个问题简单谈谈我的看法。
1 最坏的准备
国家鼓励家庭储备必要的生活物资不是为打仗做准备,而是为冬季疫情做准备!这个冬天,我们面临的疫情压力之大,可能远超普通人的想象。
这么说吧,为了应对冬季疫情的压力,国家已经严阵以待,某种意义上甚至可以认为,为了应对冬季疫情的压力,国家已经做了最坏的准备。
我们的压力源于境外输入性疫情。
10月23日,中国正式公布《中华人民共和国陆地国界法》(以下简称陆地国界法),该法令自2022年1月1日实施。一个全国性法律从公布到实施仅仅才2个多月的时间,可见这部法律的实施有相当的紧迫性。

(来源:中国人大网)
那么,为什么要出台这部法律?它的紧迫性又在哪里?
目前几乎所有媒体对这部法律的理解都搞偏了方向。你如果上网搜索陆地国界法,通常就是这样的标题——陆地国界法颁布,谁最着急?
然后印度就迫不及待拍拍胸口:没错,正是在下!
印度这个国家很奇葩,只要聚光灯在它身上扫一下,也不管这道聚光灯是不是只从它身上路过,总会把自己当做主角站起来,向周围挥舞双臂,一副主角明星范派头。
这一次也不例外,国内媒体炒作陆地国界法主要就是针对印度。印度媒体也闻风而动,不但对我们陆地国界法表达高度关注,甚至认为该法可能对中印边界争端产生影响。
唯恐天下不乱的外媒也拿着放大镜在我们的陆地国界法找“依据”,对于一些条款进行各种曲解。比如陆地国界法有这么一条规定:
第三十四条 国务院有关部门和边境省、自治区的各级人民政府应当采取措施维护界河(江、湖)走向稳定,并依照有关条约保护和合理利用边界水。
然后《日经亚洲评论》就在评论中认为,这就是针对印度而制定的——中国政府正在考虑在冲突期间限制水量的可能性(印度北部主要河流发源地都在中国境内),援引该法规定的“保护和合理利用”。
说实话,外媒臆想猜测简直就是无稽之谈。
只要仔细阅读这一条款,很明显,条款的目的就是维护界河走向的稳定,防止因为界河走向变化而引发边境线纷争,这与从上游控制下游流水量完全是两回事。
说句诛心一点的话,中国真要在上游控制下游的流水量有1万种办法,比如为了开发水资源修建水利设施等等——没有任何人能对此挑剔出毛病,国家何必在最敏感的边界河流做文章?
相反,有了这个第三十四条规定,反而对我国利用上游河流资源是一种约束,因为如果上游过度开发水资源,就有可能对下游界河的“走向稳定”产生不利的影响。这个条款反而体现了中国与邻国睦邻友好的诚意。
整个陆地国界法洋洋洒洒6000多字,主要法律规定都是针对已经勘定国界的边境管理。众所周知,印度是极少数还未与我国勘定边界的国家,所以,认为陆地国界法是针对印度的说法基本都是捕风捉影的胡扯!
按:正是因为印度与我国还未勘定国界,所以,我们不可能将未定国界的边境管理办法明明白白写出来,那样就相当于在与印度的边境纷争中主动捆住自己的手脚。
那么,国家出台陆地国界法的主要目的是什么呢?
是为了规范和加强陆地国界工作,保障陆地国界及边境的安全稳定!
这个官方说辞比较含蓄。
这里就直白一点谈谈我的理解。
当下与未来较长一段时间,我国边境都将面临着相当大的境外疫情输入压力!陆地国界法很大程度上就是为了解决这个问题,它出台到实施的紧迫性也是因为这个原因。
2 境外疫情输入
最近瑞丽成为全国瞩目的焦点,这个边境城市承担了空前的境外疫情输入压力。
自去年以来,这个城市先后经历了5次封城,全城停工停业停学,全市市民居家隔离累计超过180天,平均每人累计做了50+的核酸检测。
为了防控境外疫情输入,这个城市做了海量的工作,包括:
—在113公里边境线设置缓冲区,搬离边境居民213户852人,依法拆除隐患建筑77栋2.1万平米;
—封闭边境小道便道68条;
—对境内有吸毒、偷渡、犯罪前科的人实施敲门见面行动,安排专人定时上门查看(这些人员是偷渡边境的主力军)。
瑞丽过去是中缅经济交流主要通道,也是云南省经济比较发达的城市。因为疫情,这个城市经济基本停摆,但是老百姓的民生还得保障。
目前政府对8类困难群体每人每月补贴1000元,全市对特殊群体发放米面菜肉等生活物资2.3万份,防疫物资7万份,消费券300万元,为服务企业减免租金2000余万,金融企业暂缓全市企业还款还利息。
对于边境搬迁的村镇,每人每月单独补贴600元,病人有特殊照顾。
说实话,如果城市经济彻底停摆,大部分市民没有生活来源的情况下,上述民生补贴还是不大够用的。
瑞丽相当于是为全国人民作出牺牲,全国人民理当回报,别的不说,全国人民在财力与物力上给与瑞丽人民大力支持是能做到的。


 (来源:新浪网)
(来源:新浪网)
我认为,瑞丽应该视为新冠疫情的特殊“灾区”,我们慈善组织应该联合当地政府广泛开展民生救助工作。
瑞丽只是防控境外疫情输入的一个边境城市,它与缅甸接壤的边境线也不过160公里,从更宏观层面来看,中国国境线有2.2万公里!
那么,中国边境未来会不会出现更多的瑞丽?
这个可能性有!而且还不小!
入秋以来,新冠疫情在境外又有反复,特别值得警惕的是,去年抗疫的优等生(主要还是集中在亚洲国家)——包括越南、新加坡、韩国都纷纷在新型变异病毒攻击下全面沦陷,最后在巨大的经济压力下选择躺平。
也就是说,去年东亚国家应对第一代新冠病毒那套办法行之有效的措施已经无法抵御德尔塔变异病毒的冲击!
东亚优等生国家都纷纷沦陷,其它国家能抗住吗?
所以,未来我国周边邻国搞不好就会全面沦陷。
真遇到这种最坏的情况,我国边境地区面临输入性疫情压力将会非常大。
所以,出台陆地国界法让我国边境地区防范境外疫情做到有法可依就显得非常紧迫。
为了应对境外输入性疫情,国家甚至紧急颁布了一部法律!我们面临形势的严峻性就不言而喻。
3 应对疫情的完备方案
陆地国界法对于应对境外输入性疫情拿出一整套完备的法律(办法)解决方案。
按:陆地国界法出台当然不是仅仅为了防止境外疫情的输入,也有打击跨境犯罪、恐怖主义渗透等等目的,这里主要就防范境外疫情输入展开分析。
首先是封闭边境。
第四十七条 有下列情形之一的,国家可以封控边境、关闭口岸,并依照有关法律法规采取其他紧急措施:
(一)周边发生战争或者武装冲突可能影响国家边防安全稳定;
(二)发生使国家安全或者边境居民的人身财产安全受到严重威胁的重大事件;
(三)边境受到自然灾害、事故灾难、公共卫生事件或者核生化污染的严重威胁;
(四)其他严重影响陆地国界及边境安全稳定的情形。
前款规定的措施由国务院有关部门、有关军事机关和地方人民政府依照相关法律和规定组织实施。
对于境外输入性疫情,仅仅是封闭边境,关闭进出口岸是远远不够的。我国邻国大部分都是经济落后的发展中国家,疫情一旦全面爆发,当地经济必然会受到巨大的影响。
经济崩溃叠加疫情必然会促使大量境外人员往经济稳定、疫情控制得非常好的中国境内跑,我们就算是封闭边境,境外人员也可以从漫长的国境线悄悄偷渡过来。
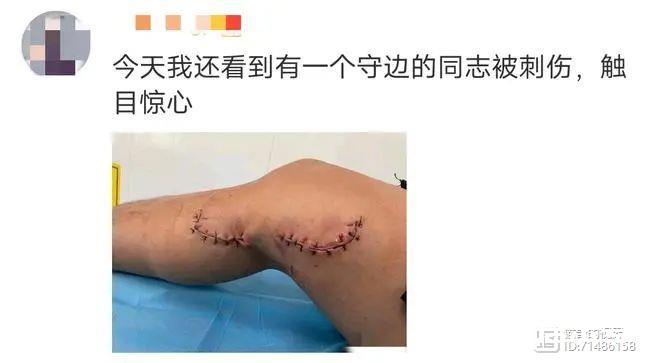
被偷渡者攻击的守边人(来源:澎湃新闻)
中国国境线长达2.2万公里,这么漫长的国境线全靠人力来守卫是不现实的,所以,在紧急时刻,还要考虑在国境线上设置拦阻设施。
第二十五条 国家根据陆地国界及边境防卫需要,可以在陆地国界内侧建设拦阻、交通、通信、监控、警戒、防卫及辅助设施等边防基础设施,也可以与陆地邻国协商后在陆地国界线上建设拦阻设施。
那么,在设施拦阻设施之后,还有境外人员不管不顾强行偷渡怎么办?毕竟,目前我国抓住偷渡人员一般就是遣返,最多也就是拘留几个月。
所以,必须在法律层面建立足够的震慑力!
第三十八条 禁止任何个人非法越界。
非法越界人员被控制后,由公安机关等主管部门处理;非法越界人员为武装部队人员的,由有关军事机关处理。
非法越界人员行凶、拒捕或者实施其他暴力行为,危及他人人身和财产安全的,执法执勤人员可以依法使用警械和武器。
很多人把这一条简单理解为针对印度非法越界行为,但是我个人理解这一条还有更为广泛的含义。比如,疫情爆发特别严重的境外地区出现大规模人员向中国境内强行偷渡,算不算“危及他人人身和财产安全的”?
如果算,那么我们边境执法人员就可以“依法使用警械和武器”。
那么,如果境外形势特别严峻,在封闭边境+设置拦阻设施+依法使用警械和武器都还不能杜绝境外偷渡的情况下怎么办?
那就只能采取更为特殊的措施。
第二十四条 国家根据边防管控需要,可以在靠近陆地国界的特定区域划定边境禁区并设置警示标志,禁止无关人员进入。
划定边境禁区应当兼顾经济社会发展、自然资源和生态环境保护、居民生产生活,由有关军事机关会同边境省、自治区人民政府提出方案,经征求国务院有关部门意见后,报国务院和中央军事委员会批准。
边境禁区的变更或者撤销,依照前款规定程序办理。
在上个世纪50年代,因为特殊的历史原因,香港当局为了防止走私与偷渡,在新界北部,毗邻深圳的区域设置了面积高达2800公顷的禁区,禁区之内不允许任何人居住与活动。
 逃往香港的难民(来源:中国国家地理)
逃往香港的难民(来源:中国国家地理)
港英当局设置禁区的考量我们姑且不论,这个禁区的设立对于防止偷渡确实达到了比较好的效果。
所以,如果境外形势恶化难以控制,比如在疫情冲击下该国经济崩溃出现向中国境内涌动的巨大难民潮——这种情况下,就可以按照陆地国界法规定,我国在边境地区设置禁区,将禁区内的中国居民迁移。
这样不但可以大幅度提高境外偷渡的难度,同时也可以应对境外难民潮有一个缓冲区。
综上所述,对于境外疫情输入国家真正是做到了高度重视,并且迅速拿出一套完整的应对办法以及法律依据,包括封闭边境+设置拦阻设施+依法使用警械和武器+设置禁区。
值得注意的是,这套应对办法与措施权力主要还是集中在中央,包括封闭边境+设置拦阻设施+设置禁区条款后面都有“由国务院和中央军事委员会批准”的规定。
这是因为边境地区比较敏感,在边境实施较大动作可能会引发邻国的强烈反应(印度:你指桑骂槐说谁呢?),所以,这些权力没有下放给地方,最后还得由中央批准。
4 共克时艰
自新冠疫情爆发以来,中国政府本着对老百姓生命负责的态度一直坚持疫情清零的策略,并且为此付出巨大的经济代价。这个坚持清零的策略在国外也引发了相当大的争议,最近外媒甚至将中国政府清零策略描述为“恐怖清零”。
国内因为经济压力也有“与病毒共存”的呼声。但是,很明显,管理层并没有因为这些压力而改变策略,陆地国界法的颁布展现了管理层坚持病毒清零策略的决心。
按照疫情发展趋势,这个冬季可能不好过,首当其冲就是国内旅游业、服务业以及中小企业,这方面国家已经有所预判,所以最近国家出台了中小企业暂缓缴纳税费的政策——当前国家财政压力如此之大,国家还出台这样的政策已经是竭尽全力了。
 (来源:新华社)
(来源:新华社)
通过前面的分析,现在我们就能正确理解这则通知的含义。
这与大家想象中的台海局势没有一毛钱关系,这是为突发疫情做准备。因为冬季疫情一旦爆发,就有很多小区随时可能封闭式管理,家庭储备生活必需品就是做这样的准备。
从紧急颁布陆地国界法到暂缓中小企业缴纳税费+商务部发布储备生活必需品的通知——国家为了应对冬季疫情已经做了万全的准备,当然也可以理解为做了最坏的打算。
所以,不要因为经济遇到暂时困难就牢骚满腹,看看境外那些深陷疫情的国家,看看边境为了防控输入性疫情而付出重大代价的城市(比如瑞丽),说实话国内绝大部分地区的人民已经算是很幸运了。
多事之秋,需要大家共克时艰。相关阅读(点击下方标题可直接阅读):
下一篇
徐文兵小课堂 | 灰指甲








