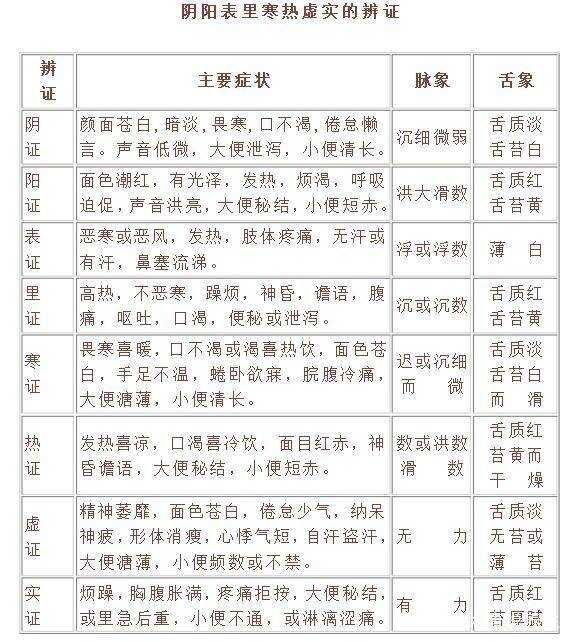
深度学习——深度学习模型的基本结构
1、全连接神经网络(Fully Connected Structure)
最基本的神经网络非全连接神经网络莫属了，在图中，a是神经元的输出，l代表层数，i代表第i个神经元。
两层神经元之间两两连接，注意这里的w代表每条线上的权重，如果是第l-1层连接到l层，w的上标是l，下表ij代表了第l-1层的第j个神经元连接到第l层的第i个神经元，这里与我们的尝试似乎不太一样，不过并无大碍。
所以两层之间的连接矩阵可以写为如下的形式：
每一个神经元都有一个偏置项：
第l层的第i个神经元的输出a是怎么得到的呢？我们首先会对上一层的所有神经元与该神经元计算一个加权平均，最后不要忘记加上偏置项。这个值记为z，即该神经元的输入。
如果写成矩阵形式如下图：
针对输入z，我们经过一个激活函数得到输出a：
常见的激活函数有：
这里介绍三个：
sigmoid
Sigmoid 是常用的非线性的激活函数，它的数学形式如下：
它能够把输入的连续实值“压缩”到0和1之间。
特别的，如果是非常大的负数，那么输出就是0；如果是非常大的正数，输出就是1，如下图所示：
sigmoid 函数曾经被使用的很多，不过近年来，用它的人越来越少了。主要是因为它的一些 缺点：
**Sigmoids saturate and kill gradients. **（saturate 这个词怎么翻译？饱和？）sigmoid 有一个非常致命的缺点，当输入非常大或者非常小的时候（saturation），这些神经元的梯度是接近于0的，从图中可以看出梯度的趋势。所以，你需要尤其注意参数的初始值来尽量避免saturation的情况。如果你的初始值很大的话，大部分神经元可能都会处在saturation的状态而把gradient kill掉，这会导致网络变的很难学习。
Sigmoid 的 output 不是0均值. 这是不可取的，因为这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。
产生的一个结果就是：如果数据进入神经元的时候是正的(e.g. x>0 elementwise in f=wTx+b)，那么 w 计算出的梯度也会始终都是正的。
当然了，如果你是按batch去训练，那么那个batch可能得到不同的信号，所以这个问题还是可以缓解一下的。因此，非0均值这个问题虽然会产生一些不好的影响，不过跟上面提到的 kill gradients 问题相比还是要好很多的。
tanh
tanh 跟sigmoid还是很像的，实际上，tanh 是sigmoid的变形：
tanh(x)=2sigmoid(2x)−1
与 sigmoid 不同的是，tanh 是0均值的。因此，实际应用中，tanh 会比 sigmoid 更好（毕竟去粗取精了嘛）。
tanh的函数图像如下图所示：
ReLu
近年来，ReLU 变的越来越受欢迎。它的数学表达式如下：
f(x)=max(0,x)
很显然，从图左可以看出，输入信号<0时，输出都是0，>0 的情况下，输出等于输入。w 是二维的情况下，使用ReLU之后的效果如下：
所以，整合一下上面说的：
2、循环神经网络(Recurrent Structure)
循环神经网络常用来处理Sequence类型的数据，比如一句话。
循环神经网络的结构如下，简单来说，我们的网络结构定义在中间的f，它每次接受两个输入h和x，输出y和h'：
当然，循环神经网络也可以有多层，网络结构如下图所示：
另外，还有双向循环神经网络的结构：
了解了各种RNN的基本结构之后，那么问题来了，f怎么定义的呢，对于一般的RNN，中间的f定义如下（下面的定义忽略了偏置项）：
3、LSTM
在RNN的基础上，还有一种常用的基本结构是LSTM，如果在RNN中，我们把输入h看成是记忆的话，LSTM将这种记忆进一步分为了长时记忆和短时记忆：
这里的c变化非常缓慢，可以认为是长时记忆，h变化非常快，可以认为是短时记忆。可以看到，LSTM的输入有三项x，h，c，输出也是三项，那么对于三项输入，LSTM内部是怎么处理的呢？
根据x和h，我们会计算出三个门，分别为输入门、遗忘门、输出门。
根据这三个门，我们可以得到LSTM的基本结构如下：
上一时刻输入的c与遗忘门进行对位相乘，选择对之前信息的遗忘程度，然后加入这一时刻的输入信息，作为这一时刻册长时记忆c输出。长时记忆经过tanh激活之后再与输出门对位相乘，作为这一时刻的短时记忆输出，h再经过一层神经网络，得到这一时刻的输出。看到这里，想清楚过程，我们可以尝试一下在纸上画一下LSTM的结构。
还有一种常用的结构，这种结构使用程度渐渐超过了LSTM，称为GRU，对LSTM网络进行了压缩，更容易训练。下面图上的公式实际是错的，右边第一项上标应该是t-1 .
4、卷积网络
卷积网络有两个重要的特性
稀疏连接 Sparse Connectivity ：每个神经元仅与前一层部分神经元相连接
参数共享 Parameter Sharing：同一个feature map的参数是相同的。
假设有100 * 100像素 的 图片，如果下一层有100个神经元，那么全连接的神经网络，将有100 * 100 * 100=100万的参数，如果采用稀疏连接和参数共享，后一层的一个神经元只与前一层的100个神经元连接，那么需要100 * 100 = 1万个参数，如果与不同神经元连接的这100条线的参数都相同，那么只需要100个参数，这叫一个feature map或者说一个field，但是这只能学到一个特征，我们可以定义多个feature map来学习不同的特征，如果有100个feature map，那么参数就是100 * 100的量。
如下面的图中，我们定义了两个feature map，红橙黄连线上的参数是共享的，蓝绿连线上的参数是共享的。
上面是卷积的概念，在卷积神经网络中，还有一个重要的概念是池化：Pooling，即将几个神经元的输出变为一个输出，池化的方法有平均法、最大值法和L2法。
视频中还讨论的一个点是，我们该拿哪些结果进行池化，可以是同一个feature map出来的，也可以组合不同feature map出来的。
最新文章
-
揭秘：伤寒汗出病解的方式有哪些
6分钟前 -
洗髓修炼中的：找病、攻病、翻病、愈病！
21分钟前 -
（原创）颤证的经方治疗案。。。
27分钟前 -
中医教你：看指甲上的月牙诊病
39分钟前 -
中药方论（24）
42分钟前 -
仅一味中药就可以降血糖 ，一味中药的单药方！
44分钟前 -
解郁安神颗粒：抑郁症、焦虑症都是因为肝的疏泄功能出现了失调
55分钟前 -
有一种痛苦叫牙疼，有种止疼药叫艾灸！收藏起来，以备不时之需！
1小时前
有话要说...