当前位置：首页 > 财经 > 正文

考夫曼自适应均线指标公式和原理详解|系数|dma

考夫曼自适应均线(KAMA)由佩里·考夫曼发明的，与传统的均线相比，考虑了价格的波动性，可以过滤小幅波动造成的市场噪音，减少错误信号。当价格波动性较低时，考夫曼自适应均线会保持在当前价格附近；当波动性增加时，自适应均线将进行调整，以稍远的距离跟踪价格，可用于识别整体趋势、把握趋势转折点和过滤价格走势。

一、考夫曼自适应均线原理

考夫曼自适应均线的原理和EMA均线有点类似，都是以平滑系数来调节权重，但与EMA的系数不同。EMA均线平滑系数是2/(N+1)，N是周期数，对于某一条均线，这个系数是固定的。比如20日EMA均线，N就等于20，平滑系数就是2/21。而考夫曼自适应均线的平滑系数是可变的。

EMA公式：

今日EMA = 2/(N+1)x今日收盘价 + (1-2/(N+1))x昨日EMA

考夫曼自适应均线KAMA计算公式：

今日KAMA = 昨日KAMA + SC x (今日收盘价-昨日KAMA)

变换一下，得到：

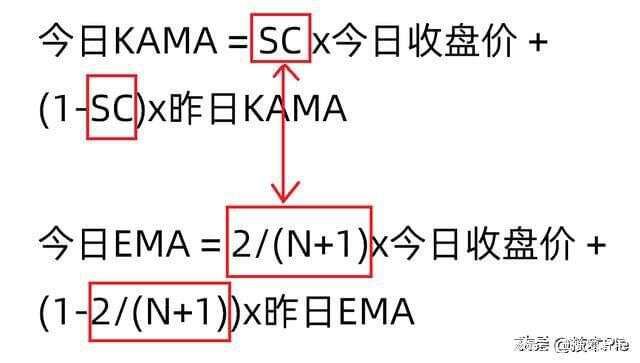
今日KAMA = SC x今日收盘价 + (1-SC)x昨日KAMA

通过下图对比，可以看出KAMA和EMA的区别。

考夫曼自适应均线指标公式和原理详解|系数|dma

二、DMA函数

考夫曼自适应均线的公式比较复杂，如果直接按照公式写，很难实现。但是通达信自带了DMA函数，可以很好的解决这个问题。

DMA函数

含义：求动态移动平均。

用法：DMA(X,A)，表示求X的动态移动平均。

DMA的算法是Y=A*X+(1-A)*Y'，其中Y'表示上一周期的Y值，A的取值范围是0-1。

通过变换之后的公式，今日KAMA = SC x今日收盘价 + (1-SC)x昨日KAMA，用DMA函数很容易就能写出来，DMA(C,SC)。

根据DMA(C,SC)可以看出，要得到考夫曼自适应均线，必须先计算平滑系数，而平滑系数又是根据效率系数计算的。因此首先来了解效率系数。

三、效率系数

效率系数ER代表价格变化的效率，用价格变化除以波动。价格变化为收盘价与M日前的收盘价之差，波动为M日的收盘价与昨日收盘价之差的绝对值之和。（参数M缺省取值为10）

:=ABS(CLOSE-REF(C,M));:=SUM(ABS(CLOSE-REF(C,1)),M);ER:=/;

以M=10为例，当收盘价与10日前的收盘价相同时，效率系数ER等于0；当最近10天每天都上涨或者每天都下跌时，效率系数ER等于1。

四、平滑系数

考夫曼自适应均线平滑系数的最初形式也是类似于EMA均线的2/(N+1)，最快的平滑系数N取2，最慢的平滑系数N取30，根据不同节奏的行情，用相应的效率系数来调节平滑系数。

最快的平滑系数=2/(2+1)=0.667

最慢的平滑系数=2/(30+1)=0.0645

最初形式的平滑系数=ER*(-)+

通过公式可以发现，当效率系数ER接近于1时，最初形式的平滑系数的值接近于最快的平滑系数；当效率系数ER接近于0时，最初形式的平滑系数的值接近于最慢的平滑系数。

考夫曼通过测试发现，对最初形式的平滑系数进行平方之后，可以改进结果。

最终的平滑系数SC= x

:=2/(N1+1);:=2/(N2+1);:=ER*(-)+;SC:=POW(,2);

五、考夫曼自适应均线

得到效率系数和平滑系数后，就可以计算考夫曼自适应均线KAMA了。

KAMA:DMA(C,SC);

另外为了方便使用，可以对考夫曼自适应均线进行处理，上涨时显示红色，下跌时显示绿色，并加粗显示。

KAMA:DMA(C,SC),,;:IF(KAMA

你可能想看：

【案例】如何让孩子爱上数学？洋葱数学的自适应趣味课堂分析

很多孩子都对数学这门学科存在畏难情绪，这个帮助学生提高学习数学兴趣”以100%人机交互学习的教学创新模式、优质视频课程内容的自适应学习体验，洋葱数学在产品上摒弃用真人教师直播授课。洋葱数学是如何提高孩...

TRIZ理论的40个发明原理详解

物理冲突是指一个物体有相反的需求，3．局部性质原则 a．从物体或外部介质(外部作用)的一致结构过渡到不一致结构，b．物体的不同部分应当具有不同的功能，c．物体的每一部分均应具备最适于它工作的条件，b...

通达信稳赚不赔指标公式

'抄底');10)AND COUNT((值<,'买入');'减仓');'轻仓');87.5);'逃顶');值*0.9;STICKLINE(V/MA(VOL;2) AND C/EMA(C;20)&l...

通达信MACD背驰缠论指标公式

=FINANCE(34);=EMA(CLOSE,10)-EMA(CLOSE;=EMA(DIF;=2*(DIF-DE);DIFF:DEA:IF(↓<,DIFF;'低');=CROSS(DIFF;=C...

通达信指标公式编写教程[完整版]

O)*100>=B}:1)*1.099;NOT(C>CROSS(周J;C:C=REF(C;C/REF(C;高开低走;O>:REF(C;REF(H:下跳空;MIN(O;MAX(O:C)

通达信绝对真底指标公式

=EMA(VAR6,=IF(VAR6

通达信黄金分割下降主图指标公式（牛回头利器）

N:=FILTER(A1;=FILTER(C1;=E1>,=FILTER(A2;=FILTER(C2;=BACKSET(ISLASTBAR;REF(E2;=REF(H,N2)=HHV(H;=BAC...

黄金柱主图指标公式（按王子老师的《量线捉涨停》的理论设计的主图，供大家研究使用）

O;L:=MA(VOL;=MA(VOL,REF(VOL40:=REF(COUNT(C

通达信底部主升起爆选股指标公式

=SMA(RSV2;=(CLOSE-LLV(LOW;=STICKLINE(中线<,=STICKLINE(短线<,=(EMA(CLOSE;8)-EMA(CLOSE:=(CLOSE-VAR3)/V...

通达信指标公式——至今为止最全的

IF(多头线>=REF(多头线;=空头线;REF(CLOSE;DRAWTEXT(VAR1>=REF(EMA(DMA((((HIGH + LOW) + (CLOSE * 2)) / 4.09):DRAW...

电容补偿柜的作用和原理

如何计算无功补偿电容柜所需要多大的电容器,如变压器为200KVA补偿电容容量为60-80KVAR.，用于补偿发电机无功电流、减轻发电机工作负荷，电容柜工作原理 用电设备除电阻性负载外，大部分用电设备均...

指标BBI、EBBI和MACD还有均线是什么意思？_疯股哥上海

指标BBI、EBBI和MACD还有均线是什么意思？是通过将几条不同天数移动平均线用加权平均方法计算出的一条移动平均线的综合指标，ＢＢＩ指标本身就是针对普通移动平均线ＭＡ指标的一种改进。多空指数的数值分...

优品公式指标（走强策略），通宵研究主力动向，抵不过指标的稳定

=(((CLOSE - REF(CLOSE;1)) / REF(CLOSE:18)) / (HHV(HIGH;=SMA(VAR4;=LLVBARS(LOW:=HHVBARS(HIGH:VAR10;=S...

基尼系数如何计算？

官方发布的基尼系数与切身体会大相庭径！不仅仅穿衣吃饭这么简单，人民健康第一的意识不断加强，医疗保健和健身的开支往往很大；为了提高生活质量，学习新知识、参加各式各样的文化娱乐活动、私家车也越来越多；休闲...

认识样式和解读

康德在十余年的专致思考中提出了认识是一种心灵方式制作。康德的学说从根本上破除了认识是客观本体反映的传统见解，这种认识的主体方式先验地存在于人类的头脑中，就是我们的头脑自身带有的具有统摄特质的时空方式和...

主题：【干货】对比融梗文和原文，学习同一个梗更高明的处理手法

魔镜和知识之书的能力都是无所不知，来测试小朋友是否够格进入学院学习——从姓名，也不知道这书是想评小男孩的忍耐能力还是脸皮厚度，所以魔镜每一次出场我们都会加深它无所不知的印象，也就是提供有效的信息帮到主...

精典图形分析，均线与macd配合使用捕捉牛品！

三次买入机会，一根大阳定乾坤，止跌企稳，站上20天线，macd零轴下白线上穿黄线金叉；为买入信号。初次碰趋势线120线回落，重新站上120线。攻击年线250后回调，重回250线上，这时macd零轴上金...

炒股到了只看“一根均线”的境界，你就可能一辈子都不会输！

要练习多长时间才能成为一个高手，你要找出能说服你做出买卖操作的理由，套在其中的股民却因没法忍受连续下跌带来的痛苦和压力，低位的时候会有资金进去接盘，那么我们投资者如何去把握买入机会呢。很多人认为均线是...

3SMA趋势交易（5）|均线或趋势线？

估计大家已经通过前面的介绍了解到3SMA趋势交易系统是怎样的一套系统和它是如何在我们的交易中发挥作用的。3SMA趋势交易系统就是一个由均线构成的趋势系统，为什么我们做交易是用均线而不是用趋势线呢？趋势...

【通达信】麟龙决策曲线JC公式指标源码（通达信版）

跌势ADX转折扣-3分;-180以下扣-2分;布林线下限以下扣-1分;45扣-3分;350加3分

【图】通达信缠论中枢指标改成KT交易师公式

C)*10000);=DRAW,DRAWTEXT_FIX((MACHINETIME1090000AND MACHINETIME1总股本:=STRCAT(STRCAT('总股本,市值:=STRCAT(S...

最精准的换手率选股法股票指标 通达信公式（附图）

换手率;VOL/CAPITAL*100 LINETHICK0;=ABS((OPEN - CLOSE)):OPEN;=((ggs10 / ggs7) * VOL):=((MA(CLOSE;10)) AN...

空调压缩机工作原理,空调压缩机的工作原理图(图)

空调能够精准调节室温与空调压缩机工作原理有关。涡旋式空调压缩机工作原理图（分步）：涡旋式空调压缩机工作原理图（动图）空调压缩机工作原理，先认识下空调压缩机的工作回路，空调压缩机的工作回路分为蒸发区和冷...

零售行业数据指标体系详解！建议收藏

我们通过在各种渠道上吸引客户来购买我们的商品来实现盈利的目的，在我们运营的每个环节都可能影响到销售额，它需要一个立体化的思维才能找到影响销售额的因素：其实线下零售的员工相当程度上担任了运营与销售的角色...

VR（成交量变异率）指标详解

是一项通过分析股价上升日成交额（或成交量，股价上涨时的成交量成为AV，股价下降时的成交量成为BV，股价不涨不跌时的成交量成为CV，则表明VR指标和OBV出现了底背离走势，则表明VR指标和OBV出现了顶...

[教程]解决由于法律原因，IDM无法下载文件的问题

常用IDM的朋友应该会见过下面这个提示框，某些视频网站上的内容无法使用IDM直接下载。一款下载m3u8流媒体的神器:下载好之后单独放一个文件夹，一、复制视频下载地址，只需刷新网页，再次点击IDM下载按...

青花五彩 DM

　金代磁州窑系烧造的釉上红、绿彩瓷器是最早的釉上五彩瓷器，景德镇窑从元代开始烧造五彩瓷器，官窑青花五彩瓷器烧成，明朝中期开始流行的青花五彩工艺，　　青花五彩瓷器烧造工艺复杂。先于坯上用青花料描绘出一定...

DMA 算法 考夫曼自适应均线 平滑系数 效率系数

上一篇
《滴天髓》解读（１５）月令

下一篇
穿山透地与分金

有话要说...

最新文章

取消
扫码支持 支付码