小白学物理之狭义相对论（6）——相对论动量和能量
上一章我们讨论了相对论速度合成公式，这一章我们讨论一下相对论动量和能量。
设想有AB两个小球，质量均为m_{0} ，两小球以大小相等方向相反的速度在O点相撞，碰撞后两小球都偏离了原来的运动方向但运动速度仍然大小相等方向相反，很显然在这个过程中动量守恒。我们选取这样一个坐标系，让x轴恰好平分小球A碰撞前与小球B碰撞后速度的夹角，如此一来，小球AB碰撞前后在x轴方向的速度分量都不变，而在y轴方向则大小不变方向相反。
现在我们驱车沿x轴以和小球A在x轴速度分量相同的速度前进，那么在车上观察小球AB的碰撞，就会发现小球A先向上后向下，在水平方向没有速度分量。而小球B会以比在静止时观察更大的速度运动，但速度方向与x轴的夹角比在静止时观察要小。将汽车参照系中小球A的速度设为v_{A} ，在x'轴的分量设为为v_{Ax'} ，在y'轴的分量设为为v_{Ay'} ，而小球B的速度设为v_{B} ，在x'轴的分量设为为v_{Bx'} ，在y'轴的分量设为v_{By'} 。很显然，v_{Ax'} 在碰撞前后都等于0，而v_{Bx'} 在碰撞前后大小不变，至少在水平方向上动量是守恒的。
那么在竖直方向上呢？至少v_{Ay'} 在碰撞前后大小不变，而v_{By'} 也在碰撞前后大小不变，但v_{Ay'} 与v_{By'} 是否也像静止参照系中那样大小相同呢？好像并不是很明显。现在让我们使用一个小技巧，这个技巧出自费曼物理学讲义，就是让我们看看从一辆行驶方向相反速度相等的车上观察小球AB会是怎样一种情况。
很显然，从行驶方向相反速度相等的车上看，小球A变成了和原来的车上小球B那样运动，而小球B变成了和原来的车上小球A那样运动。只要求出后来这辆车上小球A的速度，就可以知道原来那辆车上小球B的速度了。现在，把后来这辆车看成静止的（由于参照系平权，我们可以把任何参照系指定为静止的），那么我们就可以运用运动参照系中垂直于运动方向的速度公式来求小球A的速度，在后来这辆车上，小球A的速度在竖直方向的分量（只考虑大小不考虑方向）：
这个小技巧有点烧脑，但是可以让我们避免繁琐的数学推导，其实不引入后来这辆车，仅用静止参照系和原来那辆车的参照系的速度变换也可以求出这个结果，只不过过程实在繁琐，有兴趣的读者可以自己推一推。
现在，我们知道了小球A和小球B在竖直方向的速度分量大小不相等，那么就带来了一个严重的后果，动量不守恒。怎么办呢？只能修改动量的定义，给动量乘上一个因子1/\sqrt{1-v^{2}/c^{2} } 。
两小球在竖直方向动量分量大小相等，动量守恒，这个世界可以清净了。
在相对论提出的初期，曾经把\frac{m_{0} }{\sqrt{1-v^{2}/c^{2} } } 合在一起定义了一个新的概念动质量，后来发现这个定义是完全没有必要的，而且会引起一系列的误解，所以我们不再使用这个概念，只用静质量m_{0} 就好。
搞定了动量，让我们开始折腾能量。能量E可以通过动量P用下面的等式来定义：
将新得到的P的表达式带入，然后求积分就可以得到E的表达式了，不过等等，对于我等小白来讲，能明白上面的等式在说啥已经够强人所难了，现在让我求积分？臣妾做不到啊！那怎么办呢？没关系，不会求，可以凑！先来看看动量表达式：P=\frac{m_{0} v}{\sqrt{1-v^{2}/c^{2} } }
这个根号看着有点烦人，搞掉，两边求平方可得：P^{2} =\frac{m_{0}^{2} v^{2}}{1-v^{2}/c^{2} }
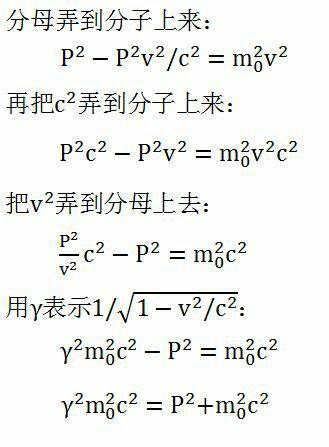
到这一步无论如何都要用到微分运算了，两边取微分：
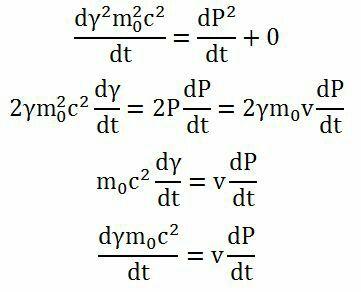
是不是挺面熟？与上面的能量动量关系式\frac{dE}{dt} =v\frac{dP}{dt} 对比，可以直接得出：E=\gamma m_{0} c^{2} ，这就是相对论能量的表达式了。当速度v=0时，\gamma =1，E=m_{0} c^{2} ，这就是著名的质能方程。
回头看一下取微分之前最后一步得到的等式：\gamma ^{2} m_{0} ^{2} c^{2} =P^{2} + m_{0} ^{2} c^{2}
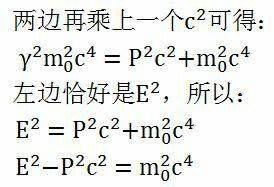
等式右边的量与参照系无关，和时空间隔一样是一个洛伦兹变换不变量。
令c=1，上式可以写成E^{2}- P^{2}= m_{0} ^{2} ，而采用这种单位制时，在不同的参照系中，能量和动量存在与距离和时间形式相同的洛伦兹变换：
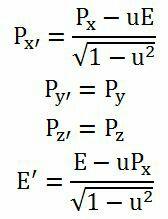
如此一来，把能量和动量合在一起就组成了一个四维矢量（E，
P_{x}
，
P_{y}
，
P_{z}
），这个四维矢量叫做四维动量，它的模方等于
E^{2}- P^{2}= m_{0} ^{2}
（c=1），它不随参照系的改变而改变。而物体所产生的引力和物体所受到的引力大小，就是由根据四维动量定义出来的能动张量决定的。接受动质量概念的人经常会有一个问题想不通，既然质量可以随速度增大而变大，那么一直对一个物体加速，会不会让这个物体变成黑洞呢？知道了四维动量是一个洛伦兹变换不变量就可以知道，这种事情是不会发生的，因为决定物体所产生的引力大小的能动张量是根据四维动量定义出来的，不会因为坐标系的改变而改变，因而也不会因速度的改变而改变。能动张量的具体定义我们以后再讨论。
最新文章
-
王长绅紫微斗数之廉贞天相在子午守财帛宫，命宫为武曲星
19分钟前 -
磁共振扫描操作磁共振冠脉成像（一）
33分钟前 -
“病急乱投医”
50分钟前 -
择日——吊用“太阳、太阴”吉神到宫的方法
1小时前 -
古诗词中的十大人生境界，古今一付笑谈中
1小时前 -
史上最全K线图大全：70种+42个K线组合图解
2小时前 -
明朝最大遗憾：崇祯若答应李自成条件，明朝不会灭亡，还灭了满清
2小时前 -
孔子语录100句（附释文）国学经典
2小时前
热门文章
-
业医必修——孙思邈《大医精诚》
1周前 -
怎样从门口看房屋吉凶
1周前 -
低估了广东的“甘蔗马蹄茅根水”，喝完半个小时就舒服了！
1周前 -
痰湿体质如何调理 最全痰湿体质调理方法(8)
1周前 -
自制家庭小咸菜
1周前 -
七彩神龙指标源码（八戒神龙主图无未来函数）
7天前 -
《奇门遁甲预测术》奇门：格局庚
6天前 -
10种朝鲜咸菜的腌制方法
7天前
有话要说...