精华收藏！深入ProE和Creo圆角的原理和应用（一）
Creo方程式曲线
方程式曲线是ProE和Creo中一种特殊形式的曲线。和其他方式创建基准曲线不同，方程式曲线是通过数学参数方程来创建的，这个特殊性也决定了它的特殊用途，在一些特殊的应用场合有着不可取代的作用。本文通过详细讲解在Creo中从简单的方程式曲线开始进行逐步演化，逐步深入，实现创建各种常见的方程式曲线的方法，务求让数学基础不太好的读者能更好地理解如何在Creo中创建自己想要而又相对复杂的方程式曲线，而非机械记住某些方程式曲线的方程。
1. 方程式曲线的创建
在Creo中，可以通过[模型]选项卡下的[基准]溢出菜单选择[曲线]菜单项，然后选择[来自方程的曲线]打开方程式曲线创建的操控面板。
要创建方程式曲线，首先要选择一种坐标系统，可以选择的坐标系统包括笛卡尔坐标、柱坐标系和球坐标系。不同的坐标系统在创建不同的参数方程时都有各自的便利性，用户需要根据方程本身的特点来选择合适的坐标系统来创建，就可以简化创建工作。
不管哪个坐标系统，都必须选择一个坐标系作为参数方程的参考，选择了坐标系后就可以进入方程式的编辑环境。第一次进入方程式曲线编辑环境时，可能会弹出有关方程式曲线编写的一些参数说明以帮助用户了解关系编写指导，你也可以随时点击顶部最右侧的信息按钮显示。
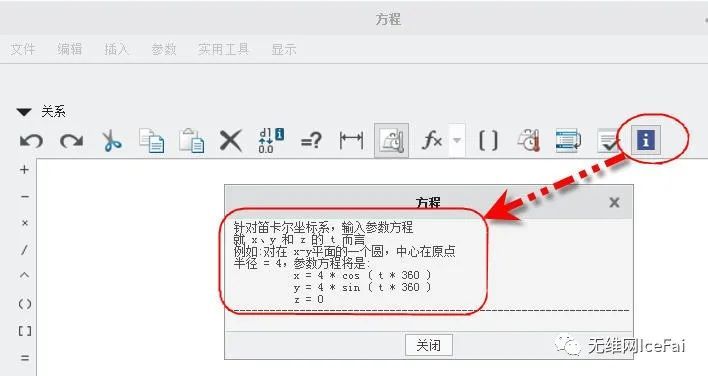
在这个编辑器中，你就可以输入你的方程式了。系统默认的设置一般方程式的编辑器是Creo自带的Pro/Tab编辑器，如果想改用系统默认的记事本来编辑，你可以设定选项：的值为。
2. 方程式的含义和编写
在Creo中，方程式的编写规则和关系式的是一样的，并且可以使用关系式的所有函数，实际上方程式本身就是关系式。
在所有的坐标系形式中，都有一个共用的可变参数t，这个实际就是用来确定方程式定义域也就是参数的取值范围的，同时也是用它来驱动方程式的生成曲线的。它的变动范围在ProE中是0~1，在Creo中用户可以自己定义。如果你对数学的参数方程式足够熟悉的话，那么理解曲线的方程式是毫无障碍的。如果你不熟悉，可以这样来看待方程式：
把方程式看成是计算某一个给定变量t所对应点的坐标值，通过t的变化实际就是产生一系列的点。连续的点就构成了实际的曲线。
2.1. 坐标系的表达方式
对于同一方程式曲线，在Creo中你都可以从三个坐标系表示方式中选择一个作为方程式的编写坐标系。三个坐标系的不同之处是确定一个点的表示方式不一样而已。
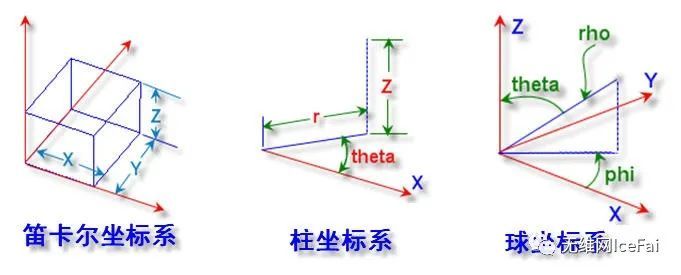
笛卡尔坐标系使用点的三个轴的坐标值（x,y,z）来确定一个点（；圆柱坐标系使用半径r，和x轴的夹角theta和高度z来表示；而球坐标系则使用球半径rho，原点到点的向量和Z轴的夹角theta和向量在xy平面上和X轴的夹角phi来表示。
2.2. 方程式中的常用函数
主要使用的是一些数学函数。
sin 正弦函数 sqrt 开平方根
cos 余弦函数 abs 取绝对值
tan 正切函数 pi 圆周率3.…
3. 实例方程式曲线剖析和演化
我们就从一个简单圆开始。我们都用笛卡尔坐标系（）坐标系来写。我们知道正弦和余弦函数是周期变化的函数，所以我们如果要实现周期变化就要借助这两个函数的帮助。而要实现值的变化，自然需要使用t来辅助了。基本上很多貌似复杂的效果都是周期变化加上大小变化的叠加。
下面我们就从一个简单的圆曲线开始，讲解如何通过各种参数的变形组合来实现更多复杂的曲线方程的。在下面的案例中，都采用默认的t从0到1的变化范围。而为了方便大家观察，曲线都扫描成了类似电缆的实体。
对于一个平面圆来说，显然z始终为恒定值，只需变化X和Y便可，以笛卡尔坐标系为例，对应的参数方程如下：（在XY平面上创建一个以原点为圆心，半径为10的圆）
x=10*cos(t*360)
y=10*sin(t*360)
z=0
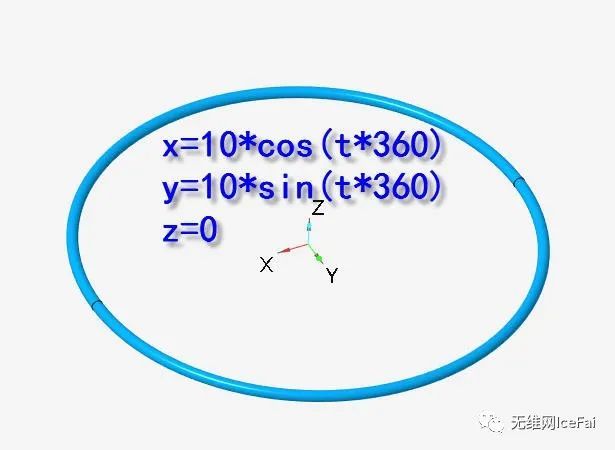
当然如果z给定一个值的话，就是圆的平面的高度了。t*360是实现角度从0到360度变化（一周）的关键。
上面的半径是维持恒定的10，如果我们添加一些变量使得半径发生周期变化，比如正弦周期变化，比如下面的方程式：
x=(10+2*sin(t*360*12))*cos(t*360)
y=(10*2*sin(t*360*12))*sin(t*360)
z=0
其中(10+2*sin(t*360*12))正是实现半径的周期变化部分，sin(t*360*12)在t从0到1的变化过程中实现了12个从-1到1的周期的变化。
而如果我们把上一步中的周期变化部分加到高度Z而不是半径上，那就实现了圆周波浪线的创建。因为半径始终保持不变，但圆周上的点高度则发生了周期变化。
x=10*cos(t*360)
y=10*sin(t*360)
z=2*sin(t*360*12)
z部分的值代表了高度值在一周内实现12个周期变化，在－2和2直接实现正弦变化。
如果把上两步的变化组合起来，我们就可以得到一个锥形的波浪线。那是因为半径和圆周上的点发生了同步的周期变化
x=(10+2*sin(t*360*12))*cos(t*360)
y=(10+2*sin(t*360*12))*sin(t*360)
z=2*sin(t*360*12)
分析很简单，显然当z处于最低的时候，圆的半径也是最小的，反之也亦然，因为他们的变化是同步的，所以就出现了这样的锥形效果
而如果我们把上一步中z的表达式改为2*cos(t*360*12)，那么高度和半径的变化的波峰和波谷正好错开，这样就可以得到了一个圆周的螺旋线圈。
x=(10+2*sin(t*360*12))*cos(t*360)
y=(10+2*sin(t*360*12))*sin(t*360)
z=2*cos(t*360*12)
上面的变化都是x和y方向的参数值都是一样的，因此在XY平面上的投影是一个正圆，如果我们改成不一样的，就可以实现椭圆周的变化了。
x=(15+2*sin(t*360*12))*cos(t*360)
y=(10+2*sin(t*360*12))*sin(t*360)
z=2*cos(t*360*12)
前面我们的变化都是封闭的，也就是说终点和起点是重合的，如果我们前面平面圆的方程稍微改一下，让z的值跟随t实现线性增加，就可以实现螺旋变化。
x=10*cos(t*360*12)
y=10*sin(t*360*12)
z=12*2*t
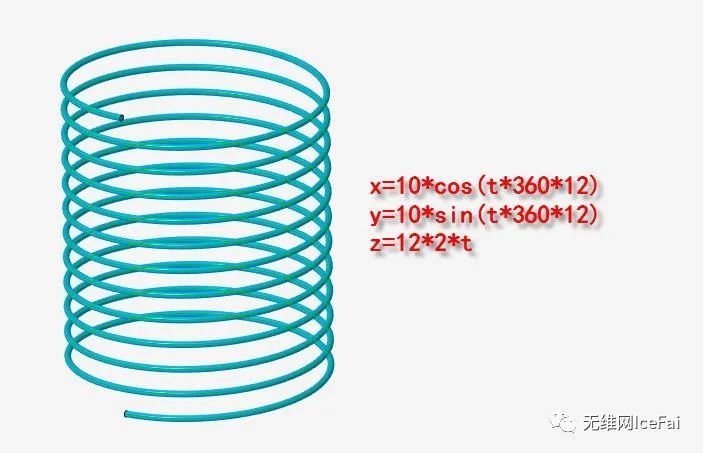
因为对螺旋线来说，高度是一直在线性增加的，而x,y是多个周期变化的。
同样，我们如果把x和y的半径纸改为不一样的就可以实现椭圆螺旋线的创建。
x=15*cos(t*360*12)
y=10*sin(t*360*12)
z=12*2*t
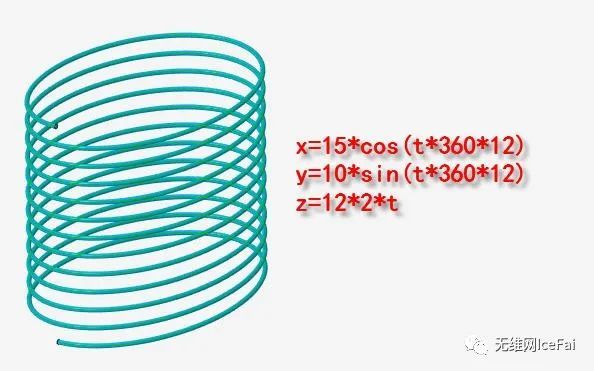
而如果我们再加上半径的大小变化，让它随着高度逐渐变小，就可以实现锥形变化，得到椭圆锥螺旋线
x=（15－14*t）*cos(t*360*12)
y=(10-9*t)*sin(t*360*12)
z=12*2*t
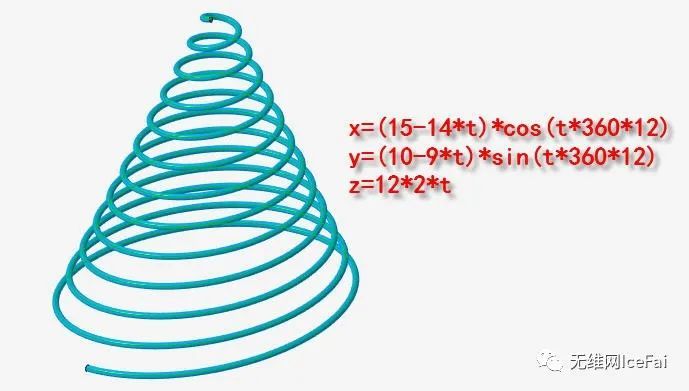
当然，如果让半径随高度实现正弦变化，就可以得到类似花瓶状的螺旋线。
x=(10+4*sin(t*360))*cos(t*360*12)
y=(10+4*sin(t*360))*sin (t*360*12)
z=24*t
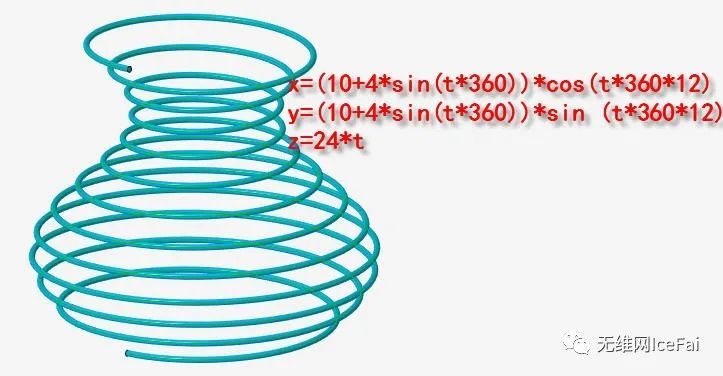
通过上面我们的演变和叠加，相信大家对于曲线方程式的概念和编写有了一定的概念了。上面我们的方程都是用笛卡尔坐标来进行编写方程式的，其实有一些我们应用其它的坐标方式来写的话就会更直接和直观，比如对于圆螺旋，我们如果用圆柱坐标系来写的话，就可以这样：
r=10
theta=t*360*12
z=24*t
这是不是比上面的笛卡尔坐标系的写法简单和直观的多呢？同样对于另外的方程式曲线，我们用球坐标的方式来写就可以收到奇效
例如对半球螺旋线，如果我们用球坐标的方式来写，就可以写成这样：
rho=10
theta=t*90
phi=t*360*12
这样是不是更为直观些呢？
而假设在theta角度上添加一些变化，又可以实现新的效果叠加
rho=30
theta=20+70*t+sin(t*360*1000)
phi=t*360*12
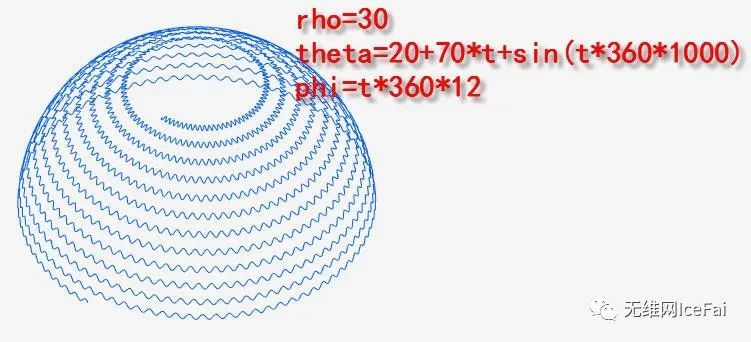
在这个方程式中，角度theta会在生成过程中发生幅度为1的正弦变化。最后累加成如图右边的效果。因为对于每一个圆周跳动的频率都是固定的所以越是靠近顶部显得越为密集。
rho=30
theta=20+70*t+sin(t*(500+600*t)*360)
phi=t*360*12
为了把在每一周上的密集度都显得差不多，可以考虑把跳动的频率越往下便相应增加，因此添加500+600*t的关系，表示从开始是500，到最后是1100，这样可以在一定程度上抵消因为半径变化所带来的密集程度的变化以实现更均匀的效果。
4．特殊曲线的方程式
其实方程式曲线的用途通常是用于创建一些有特殊几何意义的曲线的，不过，实际上这些曲线的创建已经不再是软件上的事情了，更多的是数学和几何上的意义了，我们要做的只是把它的数学公式照搬下来的体力劳动了。下面我们就来看看一些典型的曲线的方程式表示。
抛物线：数学函数是y^2=2*p*x；焦距：p/2
x=10*t
y=sqrt(2*4*x)
z=0
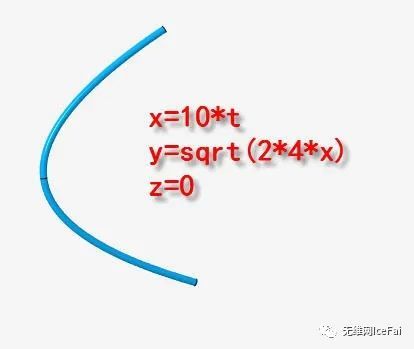
抛物线常用于灯具的反光杯，使用方程式创建可以直接根据实际需要的参数来确定方程。
阿基米德螺旋线：
k=pi/180
theta=t*360
r=k*theta*3
注意的是，这里的角度是实数，所以要注意转换一下。
渐开线：
k=pi/180
u=t*90
x=20*cos(u)-20*k*u*sin(u)
y=20*sin(u)+20*k*u*cos(u)
z=0
20是渐开线的基圆半径，u也是实数角度值.渐开线通常用于绘制齿轮。
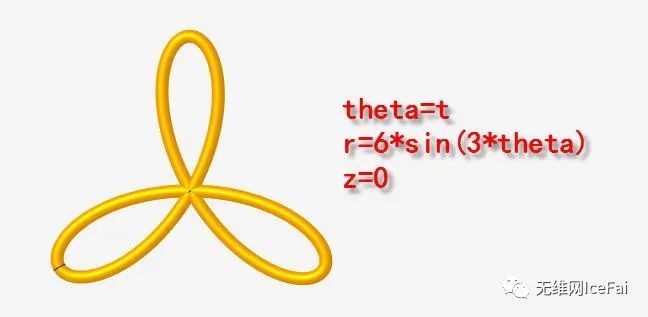
三叶玫瑰线：
theta=t
r=6*sin(3*theta)
z=0
以上内容为冰大原创作品，欢迎大家阅读和留言评论，如果觉得对你有帮助，顺手点赞以示支持，谢谢！
你可能还感兴趣
上一篇
五分钟等效一万步的走路法
最新文章
-
王长绅紫微斗数之廉贞天相在子午守财帛宫，命宫为武曲星
19分钟前 -
磁共振扫描操作磁共振冠脉成像（一）
33分钟前 -
“病急乱投医”
50分钟前 -
择日——吊用“太阳、太阴”吉神到宫的方法
1小时前 -
古诗词中的十大人生境界，古今一付笑谈中
1小时前 -
史上最全K线图大全：70种+42个K线组合图解
2小时前 -
明朝最大遗憾：崇祯若答应李自成条件，明朝不会灭亡，还灭了满清
2小时前 -
孔子语录100句（附释文）国学经典
2小时前
热门文章
-
业医必修——孙思邈《大医精诚》
1周前 -
怎样从门口看房屋吉凶
1周前 -
低估了广东的“甘蔗马蹄茅根水”，喝完半个小时就舒服了！
1周前 -
痰湿体质如何调理 最全痰湿体质调理方法(8)
1周前 -
自制家庭小咸菜
1周前 -
七彩神龙指标源码（八戒神龙主图无未来函数）
7天前 -
《奇门遁甲预测术》奇门：格局庚
6天前 -
10种朝鲜咸菜的腌制方法
7天前
有话要说...