上海初中生须补充的数学知识(1):韦达定理(草根详述)
- 教育
- 40秒前
- 81
韦达定理说明了一元二次方程中根和系数之间的关系.法国数学家弗朗索瓦·韦达于1615年在著作《论方程的识别与订正》中建立了方程根与系数的关系,提出了这条定理.由于韦达最早发现代数方程的根与系数之间有这种关系,人们把这个关系称为韦达定理.
在上海二期课改教材中韦达定理被移出必学内容,不得不说是一种遗憾,因为韦达定理不仅能提升学生对于一元二次方程的理解,更是高中数学学习必不可少的基础,所以成为上海初中生必须补充的数学定理之一!
公式推导

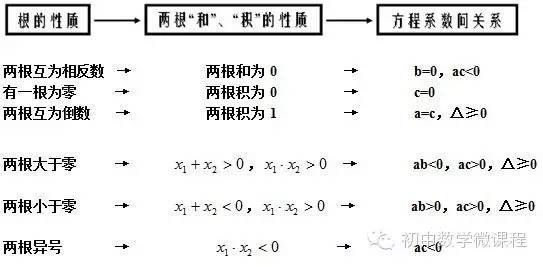
定理意义韦达定理在求根的对称函数,讨论二次方程根的符号、解对称方程组以及解一些有关二次曲线的问题都凸显出独特的作用。
一元二次方程的根的判别式为△=b^2-4ac(a,b,c分别为一元二次方程的二次项系数,一次项系数和常数项)。韦达定理与根的判别式的关系更是密不可分。
根的判别式是判定方程是否有实根的充要条件,韦达定理说明了根与系数的关系。无论方程有无实数根,实系数一元二次方程的根与系数之间适合韦达定理。判别式与韦达定理的结合,则更有效地说明与判定一元二次方程根的状况和特征。
韦达定理最重要的贡献是对代数学的推进,它最早系统地引入代数符号,推进了方程论的发展,用字母代替未知数,指出了根与系数之间的关系。韦达定理为数学中的一元方程的研究奠定了基础,对一元方程的应用创造和开拓了广泛的发展空间。例题分析


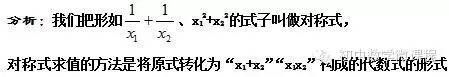


知识框架
视频讲解
(注:视频是我网络转载的,非我本人录制,推荐观看、学习)
你可能想看:








