牛顿的数学成就（之一）——二项式定理
我们应该都知道，科学家中，论伟大，牛顿可以说是数一数二的了。首先他是一位物理学家，其实主要是经典力学成就，牛顿三大运动定律（惯性定律，F=ma，作用力与反作用力定律）和万有引力定律我们耳熟能详，所以，我们也可以称他为力学家，经典力学大厦就建立在牛顿三大定律之上。其次，他是一位数学家。他作为数学家的成就一点也不逊色于他作为物理学家的成就。微积分的发明权由他与德国数学家莱布尼茨平分，这可以从至少四个方面论述，谁也不比谁差。他那个时代微积分还不叫微积分，牛顿管它叫流数术（或流数法）。他把变量叫作流，把变量的变化率叫作流数。用现在语言，流数就是导数。他的著作《流数术与无穷级数》的原著名称叫“ et '。他在数学的很多领域都有着重要的贡献。
牛顿的数学成就很多很多，今天只讲一项，那就是二项式定理。
我们大概应该知道，对正整数来说，二项式定理可以写成下面的形式：
其中的二项式系数为：
（注意，其中r=0时，二项式系数永远等于1）。下面是n=1，2，3，4，5时的结果：
注意观察，上式中标以红色的数字，它们就是帕斯卡三角形除边缘全部1以外的中间部分。好的，下面我们让a=1，b=x，则上面的二项式定理公式变为：
牛顿除研究了n为正整数的情况，他还继续研究了n为分数和负数的情况，比如
能不能也用二项式定理展开成多项式？答案是肯定的，并且可以展成无穷级数的形式。关键是二项式系数怎么处理。我们只管套用二项式系数公式即可：
比如，对n=-1，我们来写一写
的各项系数：
（请注意标红与标蓝的数字，从中可以看出这些系数是怎么写出来的。您注意到没有，每个系数中，红与蓝是颠倒的，这让我想起国外以及我国以前的一些书上，组合数C的上下角标与我们现在用的也就是这里用的是相反的。我倒是觉得以前的用法在用公式计算组合数时，上角标对应分式的生成，下角标对应分母的生成，是很顺畅自然的。这里只是提一提我的看法而已。请继续看今天的内容。）
很快就发现了规律：系数正1负1交错出现，一直下去，直至无穷。即：
牛顿把n推广到分数，举例来说，n=1/2，他得到系数如下（这里只给出了4个）：
于是得到：
牛顿让二项式定理拓展到了无穷级数，这是一项很了不起的成就，他在这上面是花了很多时间和精力的。从而微积分得以顺利发展。他之前很多悬而未解的问题，至此很多都可以解决了。
正好，我们用最后得到的这个无穷级数来完成一项任务。前不久我在本公众号中写过文章，介绍了几个用无穷级数表示圆周率π的方法，今天，我们再根据上面这个无穷级数来写出π。牛顿给出过四分之一圆面积的无穷级数表示。我简单地取圆半径为1，就可以得到π的一个新的无穷级数表示法。
首先，用负x平方（-x^2）代替上式中的x，得到：
再来看这个函数：
它表示半径为1的位于第一象限的四分之一圆周：
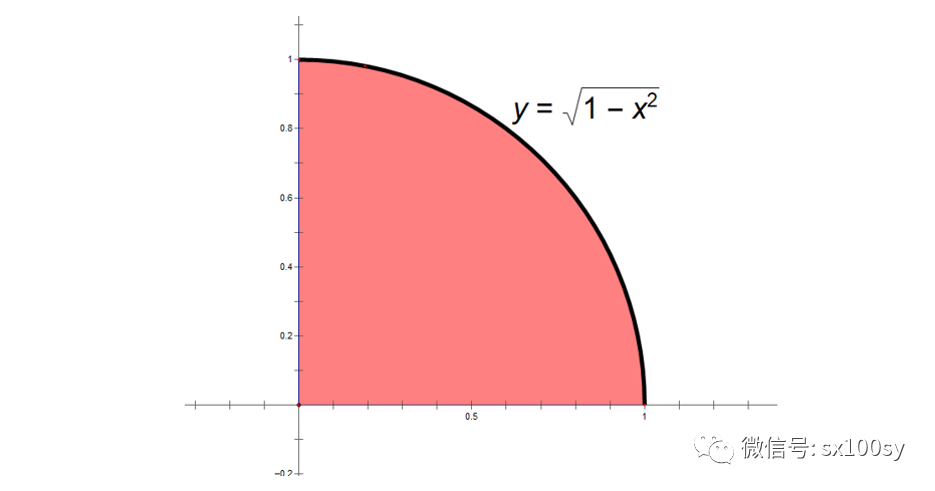
它与x轴、y轴围成的图形的面积为单位圆面积的四分之一，即π/4，用积分表示，就是：
把前面求得的无穷级数代入上面积分中，得
对每一项分别积分，最终得到
即
项数越多，结果越精确。
牛顿关注的是数学的思想和方法。微积分和牛顿三大定律是他造福人类的宏伟成就，牛顿力学直接导致了人类超越地球，走向太空。
牛顿才华横溢，又勤奋用功。他能取得伟大成就得益于他对事物的关注力，传说他精神集中做一件事，竟然忘记自己吃过饭。但他又是一们十分谦虚的人，他说他的成就只是站在了巨人的肩膀上取得的，他还说他只在一个在海边拾贝的小孩。
最新文章
-
张秀东注释
4小时前 -
北宋这些县到了金朝，为何出现治所大搬家的情况，发生了什么事
4小时前 -
黑神话悟空：看懂金蝉子为啥被贬，才明白黄眉为什么要祸乱人间
5小时前 -
RSI选股方法
5小时前 -
古玉图谱 – 书格
5小时前 -
西藏和青海是如何纳入中国版图的来看吐蕃瓦解后千年历史演变
5小时前 -
炒股秘籍，实图讲解MACD指标，零轴金叉技巧选出买点！
5小时前 -
请你欣赏宋代名画------晴春蝶戏图
5小时前
有话要说...