初中几何模型训练05之辅助线添加
其中几何的难点之一是添加辅助线，辅助线的添加并非无规律可寻。今天周老师就以初二中常见的“半角模型”，教同学们如何利用旋转思想，更快速更准确地添加辅助线，从而解决问题。
模版
手拉手模型
那么“手拉手模型”如何用旋转全等变换、转换线段来理解呢？
例2：（1）如图1，锐角△ABC中，分别以AB、AC为边向外作等腰△ABE和等腰△ACD，使AE=AB，AD=AC，∠BAE=∠CAD连接BD，CE，试猜想BD与CE的大小关系，并说明理由.
（2）如图2，四边形ABCD中，AB=7cm，BC=3cm，∠ABC=∠ACD=∠ADC=45°，求BD的长.
↑↑↑
此题是我们经常遇到的“手拉手模型”，第一问中两个等腰三角形“大手拉小手”全等易证。而第二问我们需要去模仿，尝试添加辅助线去构造另一个等腰直角三角形从而产生“手拉手模型”。
那么我们如何利用旋转思想分析第二问呢？
[分析]
求线段长度多用勾股定理，BD不在直角三角形中无法直接求出。结合“AC=AD”，所以旋转含有线段BD的△ADB。
利用“AD=AC”，起始位置AD，目标位置AC，将△ADB绕着点A顺时针旋转90°。故辅助线添加：作点B’使得AB’=AB且AB’⊥AB，易证△ABD≌△AB’C，得BD=B’C。△B’AB是等腰直角三角形求得BB’，最后证明△B’BC是直角三角形利用勾股定理求得线段长度。
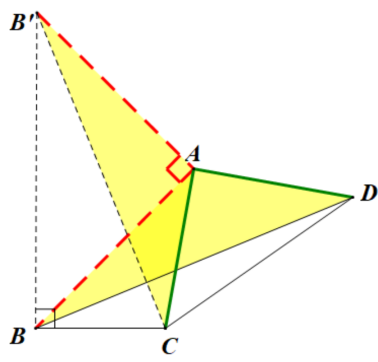
答案：√107
练习3：如图，△ABC是等边三角形，三角形外有一点D，∠ADC=30°，AD=3，BD=5，则CD的长为.
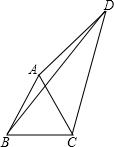
[分析]
求线段长度多用勾股定理，CD不在直角三角形中无法直接求出。故转换CD位置，选择旋转含有线段CD的△ADC。
利用“AC=AB”此天然条件，起始位置AC，目标位置AB，将△ADC绕着点A顺时针旋转60°。故辅助线添加：作点D’使得AD’=AD且∠DAD’=60°，证明△ACD≌△ABD’，得CD=BD’。由于60°的等腰三角形是等边三角形，得AD=DD’。三条线段AD、BD、CD转化到△BDD’中，证明△BDD’是直角三角形利用勾股定理求出线段长度。
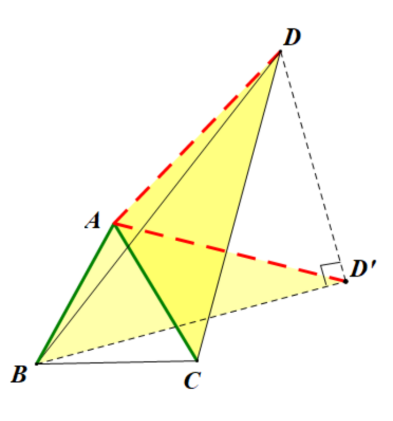
[思考]
①我们利用“AC=AB”这个“共顶点等线段”的突破口将△ADC绕点A旋转变化，那么同样的，“AC=BC”，是否也可以利用这个“共顶点等线段”的条件将△ADC绕着点C旋转呢？
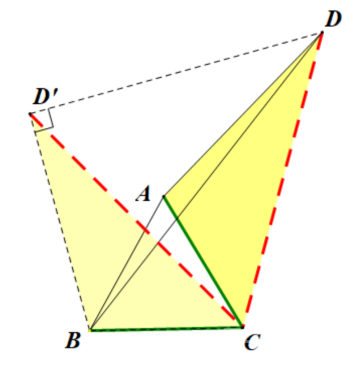
②含有线段CD的还有△BDC，那么“BC=BA”，“BC=AC”，尝试将△BDC分别绕着点B、点C旋转，是否也是两种不同的解法，同学们动手画图尝试一下吧！
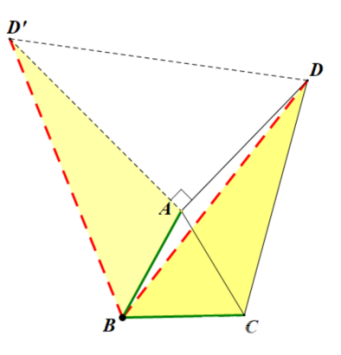
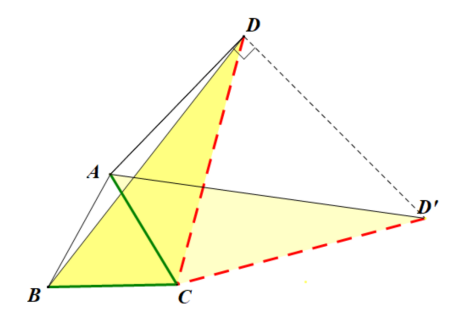
③更深入的思考，如果转化AD、BD的位置，旋转△BAD，“AB=AC”，“AB=CB”，这也是给旋转提供了天然条件，此解法最后证明△CDD’为直角三角形，这里同学们需要去思考一下怎么证明哦。
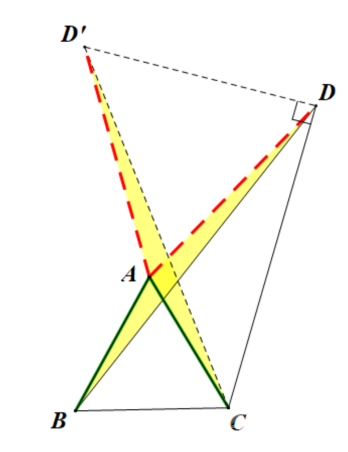
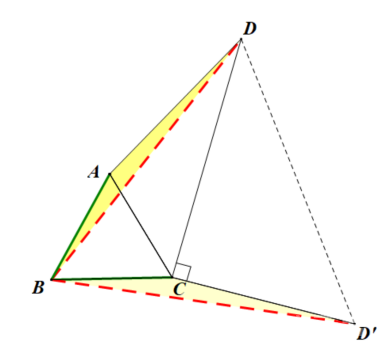
综合6种方法来看，最终我们都能成功转化线段，并结合题意证明直角三角形求出线段长度。但是由于题目条件给了∠ADC=30°，并且目的是求CD，所以综合条件与△ADC关系最为紧密，所以尝试旋转△ADC最具有目的性。
答案：4
练习4：如图，在△ABC中，∠ACB为锐角，点D为射线BC上一点，连接AD，以AD为一边且在AD的右侧作正方形ADEF。
（1）如果AB=AC，∠BAC=90°，当点D在线段BC的延长线上时，说明BD与CF之间的关系。
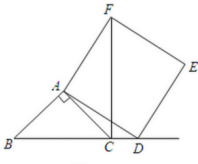
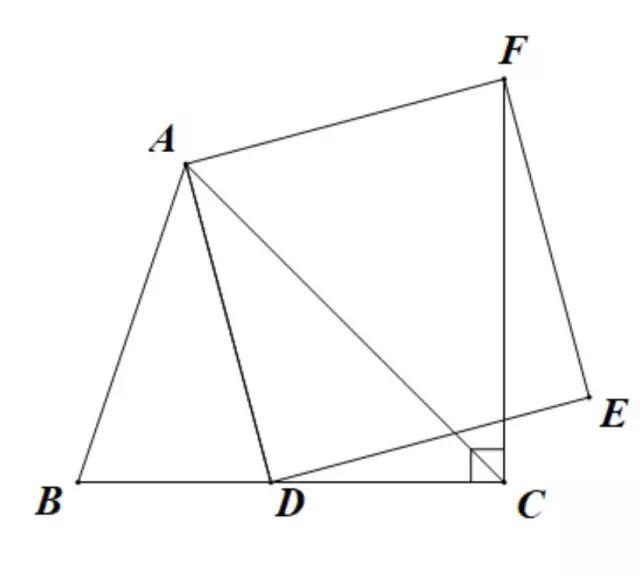
（2）如果AB≠AC，∠BAC是锐角，点D在线段BC上，当∠ACB满足什么条件时，CF⊥BC（点C.F不重合），并说明理由。
[分析]
第一问是我们常见的“手拉手模型”，利用全等易证。第二问中，条件相对分散无法直接求出∠ACB，尝试将∠ACB转化，含有∠ACB的是△ACD，那么正方形中边长“AD=AF”，此“共顶点，等线段”创造了旋转的天然条件。
起始位置AD，目标位置AF，将△ACD绕着点A逆时针旋转90°。故辅助线添加：作点C’使得AC’=AC且AC’⊥AC，易证△ADC≌△AFC’，得∠ACD=∠AC’F。需要证明C’、F、C在同一直线上，那么△ACC’为等腰直角三角形，最后求出角度。
几何是初中数学非常重要的内容，
一般会在压轴题中进行考察，
如果掌握几何模型及其构造方法，
能为考试节省不少时间，
上一篇
罗盘的使用
最新文章
-
打民事官司程序流程
9小时前 -
善式百科：一天吃一餐的9大好处！
9小时前 -
灵魂的修炼
9小时前 -
真正聪明的人：不闻人非，不视人短，不言人过！
10小时前 -
经典｜国画用墨技法
10小时前 -
百病之源——湿邪的辨识与调理
10小时前 -
知青 | 朱新地：从昆明下放傣族边寨，我们一路走了七天
10小时前 -
贾谊的短暂人生 告诉你逆商多么重要
11小时前
热门文章
-
王根权品评书谱第59讲 厥用斯弘
1周前 -
茶不会说话，却足以治愈所有
1周前 -
中国为什么要每年花20亿进口腰果中国自己种不出来腰果吗
1周前 -
历史学习记忆十法
1周前 -
临安这么有历史感，为何改名杭州
5天前 -
第04章 占婚姻
6天前 -
四味药，消息肉，鼻息肉、胃息肉、胆息肉、肠息肉…各种息肉
1周前 -
芝麻量寻牛股（附通达信、同花顺选股公式源码）
1周前
有话要说...