初中几何经典模型总结（手拉手模型）
模型可以让同学更快的进入到几何之中，产生兴趣。也是近来学习初中几何不可或缺的一种重要方法。
下面给大家介绍一种经典几何模型---手拉手模型，这也是历年数学中考常考的几何压轴题型之一。
手拉手模型的概念:
1、手的判别：
判断左右：将等腰三角形顶角顶点朝上，正对读者，读者左边为左手顶点，右边为右手顶点。
2、手拉手模型的定义：
定义: 两个顶角相等且有共顶点的等腰三角形形成的图形。（左手拉左手，右手拉右手）
例如：
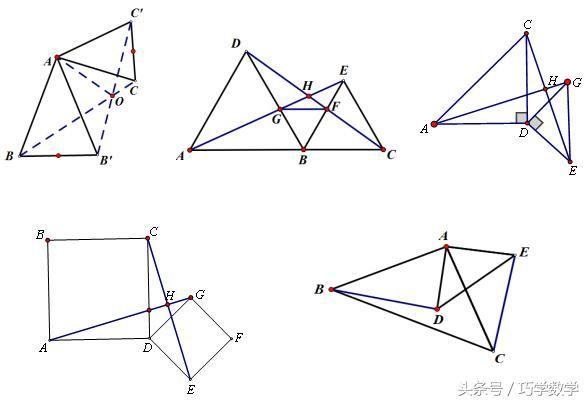
3、手拉手模型的重要结论
三个固定结论:
结论1:△ABC≌△AB'C'(SAS)
BC=B'C'（左手拉左手等于右手拉右手）
结论2：∠BOB'=∠BAB'（用四点共圆证明）
结论3: AO平分∠BOC'（用四点共圆证明）
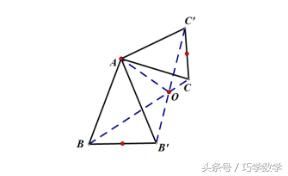
例题解析：
类型一 共顶点的等腰直角三角形中的手拉手
例1：已知：如图△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°．
求证：BD=CE．
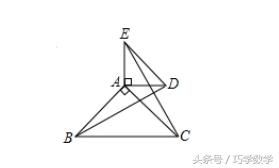
分析：
要证BD=CE可转化为证明△BAE≌△CAD，由已知可证AB=AC，AE=AD，∠BAC=∠EAD=90°，因为∠BAC ∠CAE=∠EAD ∠CAE，
即可证∠BAE=∠CAD，符合SAS，即得证．
解答：
证明：∵△ABC与△AED均为等腰直角三角形，
∴AB=AC，AE=AD，∠BAC=∠EAD=90°，
∴∠BAC ∠CAE=∠EAD ∠CAE，
即∠BAE=∠CAD，
在△BAE与△CAD中，
AB=AC,∠BAE=∠CAD，AE=AD
∴△BAE≌△CAD（SAS），
∴BD=CE．
类型二 共顶点的等边三角形中的手拉手
例2：图1、图2中，点B为线段AE上一点，△ABC与△BED都是等边三角形。
(1)如图1，求证：AD=CE；
(2)如图2，设CE与AD交于点F，连接BF.
①求证：∠CFA=60°；
②求证：CF BF=AF.
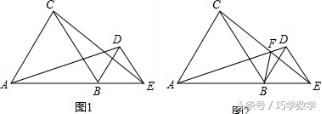
分析：
（1）如图1，利用等边三角形性质得：BD=BE，AB=BC，∠ABC=∠DBE=60°，再证∠ABD=∠CBE，根据SAS证明△ABD≌△CBE得出结论；
（2）①如图2，利用（1）中的全等得：∠BCE=∠DAB，根据两次运用外角定理可得结论；
②如图3，作辅助线，截取FG=CF，连接CG，证明△CFG是等边三角形，并证明△ACG≌△BCF，由线段的和得出结论．
解答：
证明：(1)如图1，∵△ABC与△BED都是等边三角形，
∴BD=BE,AB=BC,∠ABC=∠DBE=60°，
∴∠ABC ∠CBD=∠DBE ∠CBD，
即∠ABD=∠CBE，
在△ABD和△CBE中，
AB=AC
∠ABD=∠CBE
BD=BE，
∴△ABD≌△CBE(SAS)，
∴AD=CE，
(2)①如图2,由(1)得：△ABD≌△CBE，
∴∠BCE=∠DAB，
∵∠ABC=∠BCE ∠CEB=60°，
∴∠ABC=∠DAB ∠CEB=60°，
∵∠CFA=∠DAB ∠CEB，
∴∠CFA=60°，
②如图3,在AF上取一点G,使FG=CF,连接CG,
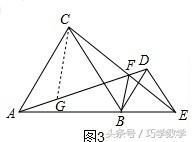
∵∠AFC=60°，
∴△CGF是等边三角形，
∴∠GCF=60°，CG=CF，
∴∠GCB ∠BCE=60°，
∵∠ACB=60°，
∴∠ACG ∠GCB=60°，
∴∠ACG=∠BCE，
∵AC=BC，
∴△ACG≌△BCF，
∴AG=BF，
∵AF=AG GF，
∴AF=BF CF.
类型三 共顶点正方形中的手拉手
例3：如图，两个正方形ABCD与DEFG,连结CE、AG,二者相交于点H。
求：（1）AG=CE （2）AG与CE之间的夹角为多少度？ （3）HD平分∠AHE
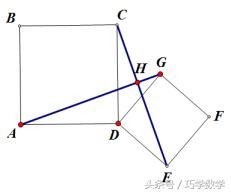
分析：
（1）由四边形ABCD与DEFG是正方形，可得AD=CD，∠ADC=∠GDE=90°，进而得出∠ADG=∠CDE，DG=DE，然后由SAS即可判定△ADG≌△CDE，根据全等三角形的性质则可证得AG=CE；
（2）根据全等三角形的性质和角的关系即可得出夹角是90°；
（3）根据全等三角形的性质和三角形的面积解答即可．
解答：
(1)∵ABCD和DEFG是正方形，
∴AD=CD,DG=DE,且∠ADC=∠GDE=90°，
∴∠ADG=∠CDE，
在△ADG与△CDE中，
AD=CD
∠ADG=∠CDE
DG=DE，
∴△ADG≌△CDE(SAS)，
∴AG=CE；
(2)CE与DG交点为O，
∵△ADG≌△CDE，
∴∠DEC=∠AGD，
∵∠DEC ∠DOE=90°，
∴∠AGD ∠DOE=90°=∠AGD ∠GOH，
∴∠GHE=90°；
(3)过点D作MD⊥AG，DN⊥CE，
∵△ADG≌△CDE，
∴S△DCE=S△ADG，
∴12×CE×DN=12×AG×DM，
∴DM=DN，且MD⊥AG，DN⊥CE，
∴DH平分∠AHE
最新文章
-
太师修行问答48：人生只是演戏瑜伽也能修禅，能达到几禅
7分钟前 -
![[书法]闲暇草书汇03](https://www.74hao.com/zb_users/upload/2024/10/202410161729086639361289.png)
[书法]闲暇草书汇03
24分钟前 -
3D技巧：两码和差选号法
46分钟前 -
“落日无情最有情，遍催万树暮蝉鸣”杨万里诗五首，风格清新自然
1小时前 -
《玄理赋》五行生克的太过不及 等
1小时前 -
《老山1984-1989，中越老山之战实录》连载之二：118团8连收敲掉54
2小时前 -
摄影：故乡的秋色（2）
2小时前 -
论入宅归火择吉（续）第二，坐向要吉 坐向要吉，主要是指所选日课
2小时前
有话要说...