初中数学之平面几何的模型与方法系列分享（一）“两形”之等边三
几何是初中数学中非常重要的内容，在中考中占分值约40%以上。而掌握几何模型能够为考试节省不少时间，这次周老师整理了常用的系列几何模型方法，一定要认真掌握哦~
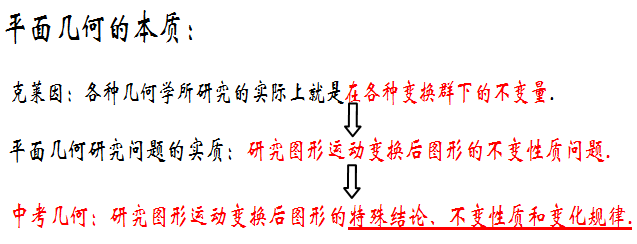
针对中考几何的三个重点（特殊结论、不变性质和变化规律），学生在学习过程中，又需要着重培养基本几何计算能力和基本几何证明能力。在几何计算方面，需要重点掌握的是：三大几何计算工具（勾股、相似、面积法）；在几何证明方面，需要重点掌握的是：三大几何变换工具（平移、旋转、轴对称）；此外，计算与证明综合，需要重点掌握的是：两形（等边三角形和正方形）、两线（中点线和角分线）和一圆（包括以圆为载体的综合计算，和以辅助圆为重点的几何证明）。
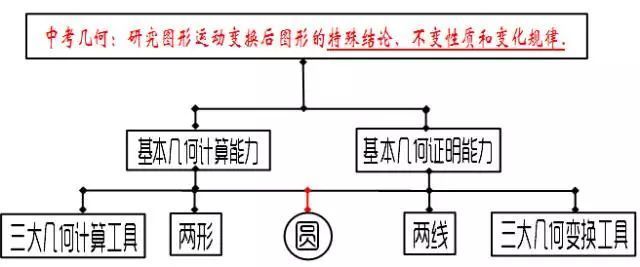
总结一下就是：三工具+三变换+两形+两线+一圆（简称33221）
对于大多数学生来说，掌握这个“33221”就足够应付中考几何了。作为老师，我们完全可以就围绕这个“33221”来建立基本的中考几何复习体系，具体学习顺序可以根据不同地域的不同情况来设计。
在掌握了“33221”的基础上，我们还需要更进一步，学习和研究以下三个专题：
1、从几何构图与命题的角度研究几何模型；2、几何最值问题（单条线段最值和多条线段最值）；
3、动态几何问题；
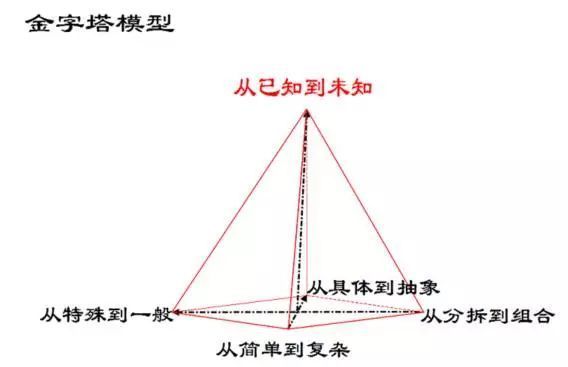
从而，最终掌握我们一开始提出的中考几何的三个重要方向：掌握图形运动变化过程中的特殊结论、不变性质和变化规律。关于数学思想方法，我曾经做过一个“四维一体的金字塔模型”讲座，后续也会分享给大家。
本期内容：
初中数学之平面几何的模型与方法系列分享（二）“两形”之等边三角形
等边三角形和正方形是最重要的两个基本图形，也是许多几何证明题的出题载体。掌握这两个图形相关的模型与方法尤其重要。本篇文章将会分享和“等边三角形”相关的几何模型，而和等边三角形相关的内容又可以分为：1、一个等边三角形相关的几何模型；2、两个等边三角形相关的几何模型。对于等边三角形的模型研究，我们首先从一个等边三角形和一个点的位置关系开始研究。（1）如图，有一个点D在等边三角形的一条边上。
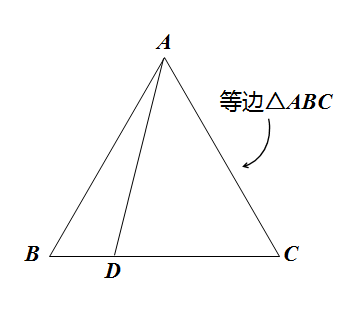
我们看看这个基本图形可以出现什么样的结论呢？大家都知道，等边三角形也是旋转的基本载体，我们可以利用旋转来进行研究。将三角形△ABD逆时针旋转至△ACE,如下图：
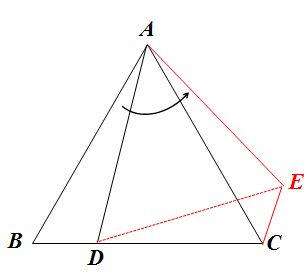
这样我们易证△ADE是等边三角形，AD=DE，同时，BD=CE，这样我们把AD、BD、CD三条线段“转移”到了一个三角形△DCE中。在同一个三角形中的三条线段，我们可以出什么题目呢？比如三边关系，CD+CE>DE，也就是说在原图形中，CD+BD>AD。
此外，还可以考察长度计算。我们容易证明∠DCE=120度，如果已知CD和CE两边的长度，就可以求出DE的长度，也就是说，原图形中，可以命题：已知CD和BD的长度，求AD的长度。（2）如图，有一个点D在等边三角形的内部，连接AD、BD、CD。
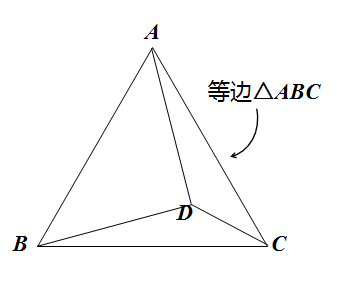
像这样，一点在等边三角形的内部，我们首先想到的应该是“费马点问题”：当点D满足什么条件时？AD+BD+CD最小。
不过“费马点问题”主要是在一个普通三角形内考察，在等边三角形这里就不用探讨了。在《旋转》部分，我们会单独讲到费马点问题。
好，我们现在依然像第一种情况一样，利用旋转来看看可以如何命题。比如下图，我们将△ADC顺时针旋转至△AEB：
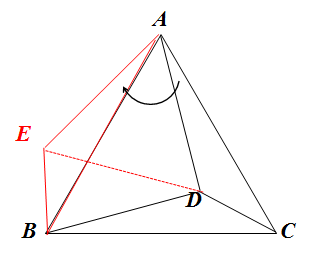
易证△ADE是等边三角形，AD=DE,这样我们就把BD、CD、AD三条线段“转移”到了一个△BDE中。这时，我们可以出什么题目呢？可以考察勾股定理啊。如果这三条边的长度刚好满足勾股定理，那么我们就能根据勾股定理的逆定理导出直角，从而可以利用三角形函数或者特殊关系导出45度、30度或60度。
比如，如果能够导出∠DEB=90度，因为△ADE是等边三角形，∠AED=60度，这样就知道∠AEB=150度，也即∠ADC=150度。
同时，用刚才的方法求出∠ADC的度数之后，我们还可以利用勾股定理求出等边三角形的边长AC。如下图：延长CD，点A做AF垂直于CD.
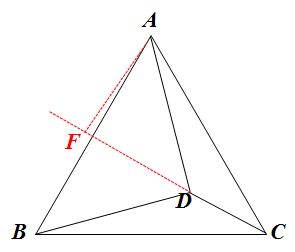
最后，除了研究边的关系，这个模型也可以研究角度的关系。比如，已知点D对三条边的“张角”-∠BDC、∠ADB、∠ADC的度数或比例关系，求以AD、BD、CD为边的三角形三个内角的度数或比例关系。关于这部分的内容我就不做详细讲述了，请各位老师自己进行研究。
所以，当一个点D在等边三角形内部的时候，我们至少有3种命题方式：1) 已知AD、BD、CD三条线段的长度或者比例关系（满足勾股定理），求∠ADC及BC；2) 已知∠ADC（150度或135度等特殊角度），求AD、BD、CD三条线段的关系；3) 已知∠BDC、∠ADB、∠ADC的度数或比例关系，求以AD、BD、CD为边的三角形三个内角的度数或比例关系。
（3）如图，有一个点D在等边三角形的外部，连接AD、BD、CD。
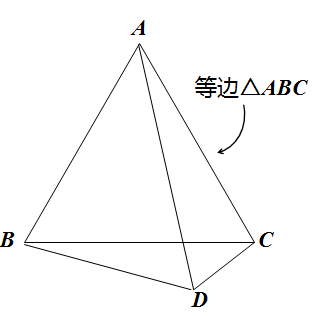
这是我们本篇文章中最重要的一种情况，会产生非常重要的一个模型。我们来一起思考和推导，还是利用旋转来看看将会出现什么情况。
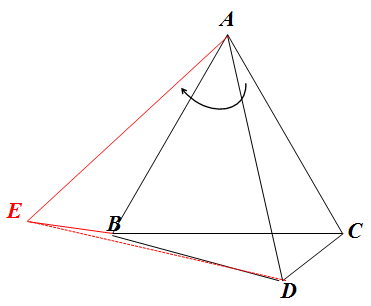
如图，我们将△ACD顺时针旋转至△ABE，连接DE。
此时，我们知道△ADE是等边三角形，AD=ED，又CD=BE，于是，AD、BD、CD三条线段转移到了一个△DBE中。可以如何命题呢？我们最容易想到的就是当E、B、D三点共线。
此时，可以导出两个重要结论：1) AD＝BD＋CD2) ∠ADB＝∠ADC＝６０度(或AD平分∠BDC)现在，让我们来重新梳理一下这个重要的模型。
模型描述：一个等边三角形外部，有一个角∠BDC＝120度。
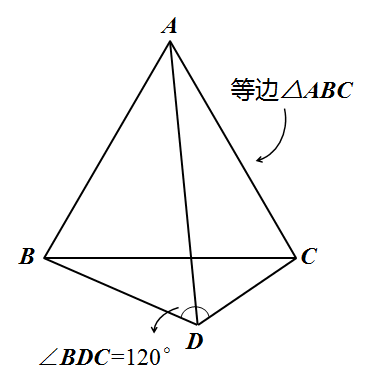
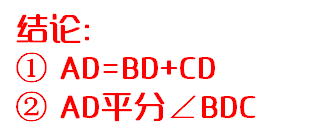
反过来，关于这个模型的证明方法，我们又可以从四个方向来证明：i. 旋转ii. 截长补短iii. 构造等边三角形iv. 角平分线
同时，这个模型还有一个变式：把已知的∠BDC＝120度变成∠ADC＝60度，上述结论仍然成立。
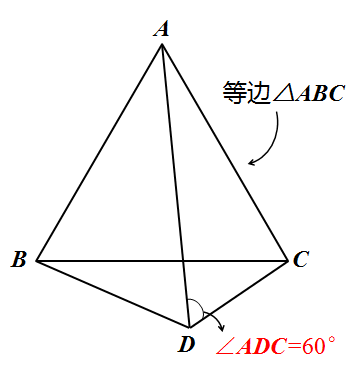
关于这个模型的一些应用场景和考题如下
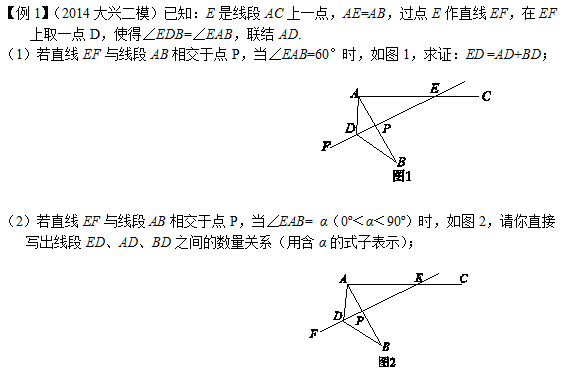
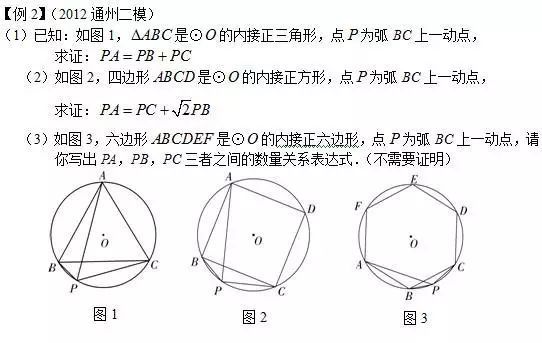
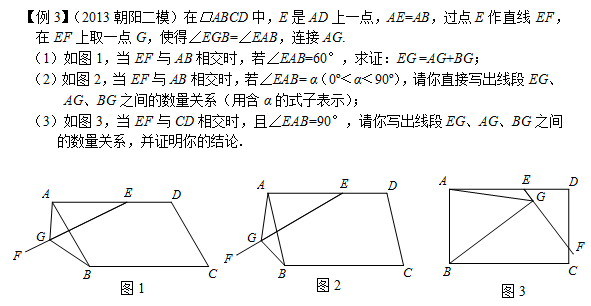
备注这几个例题中，还会涉及正方形或者等腰直角三角形的模型，我们后面会给大家做分享的。
总结这篇文章我们从一个等边三角形和一个点的位置关系出发，利用旋转为工具，去探究一个点分别在等边三角形的一边上、内部以及外部这三种不同的情况，可以如何去命题。从而总结出一些固定的结论和模型。这种研究方法可以复制和推广到其他地方，帮助我们研究和总结出更多的几何模型。
这其中，最后一种情况是最最重要的:一个等边三角形外部＋一个120度或者60度的角，可以导出一个线段和差以及一条角平分线这两个结论。
最新文章
-
王长绅紫微斗数之廉贞天相在子午守财帛宫，命宫为武曲星
19分钟前 -
磁共振扫描操作磁共振冠脉成像（一）
33分钟前 -
“病急乱投医”
50分钟前 -
择日——吊用“太阳、太阴”吉神到宫的方法
1小时前 -
古诗词中的十大人生境界，古今一付笑谈中
1小时前 -
史上最全K线图大全：70种+42个K线组合图解
2小时前 -
明朝最大遗憾：崇祯若答应李自成条件，明朝不会灭亡，还灭了满清
2小时前 -
孔子语录100句（附释文）国学经典
2小时前
热门文章
-
业医必修——孙思邈《大医精诚》
1周前 -
怎样从门口看房屋吉凶
1周前 -
低估了广东的“甘蔗马蹄茅根水”，喝完半个小时就舒服了！
1周前 -
痰湿体质如何调理 最全痰湿体质调理方法(8)
1周前 -
自制家庭小咸菜
1周前 -
七彩神龙指标源码（八戒神龙主图无未来函数）
7天前 -
《奇门遁甲预测术》奇门：格局庚
6天前 -
10种朝鲜咸菜的腌制方法
7天前
有话要说...